Tableau de capacité variable¶
Principe¶
Trois attributs sont nécessaires
- l'addresse variable de début des données
- la capacité variable
- la taille variable
Ce sont les mêmes attributs que pour un tableau de capacité fixe, mais deux d'entre eux sont maintenant variables et plus constants
- la capacité
- l'emplacement mémoire où l'on stocke des données
On peut donc réutiliser le tableau de capacité fixe comme base
import include.tableau_capacite_fixe as h
class Tableau:
def __init__(self):
self.data = []
self.capacite = 0
self.taille = 0
# Methodes de tableau de taille fixe
__str__ = h.convertir_en_texte
__len__ = h.taille
__getitem__ = h.lire_valeur_indice
__setitem__ = h.ecrire_valeur_indice
def __pop__(i = -1):
if i >= 0: h.supprimer_en_position(self,i)
else: h.supprimer_en_queue(self)
Mais nous n'utiliserons plus la fonction
def verifier_place_disponible(T,besoin = 1):
if T.taille + besoin > T.capacite:
raise Exception("capacité insuffisante")
En cas de capacité insuffisante, on l'augmentera sans que cela ne perturbe l'exécution. Ce changement concerne donc les fonctions
inserer_en_queue(T,valeur)inserer_en_position(T,indice,valeur)redimensionner(T,taille_demandee,valeur = 0)
à laquelle on ajoutera éventuellement une fonction reserver_capacite(T,capacite).
Insérer en queue¶
On remplace l'appel à verifier_place_disponible par le code augmentant la capacité
La stratégie la plus courrante consiste à passer de 0 à 1, puis à doubler la capacité si nécessaire.
Il ne faut déplacer le contenu de l'ancien au nouvel espace en mémoire, et - si le langage le demande - détruire l'ancien espace.
def inserer_en_queue(T,valeur):
if T.taille >= T.capacite:
T.capacite = 2 * T.capacite if T.capacite > 0 else 1
tmp = [None]*T.capacite
tmp[0:T.taille] = T.data[0:T.taille]
T.data = tmp
T.data[T.taille] = valeur
T.taille += 1
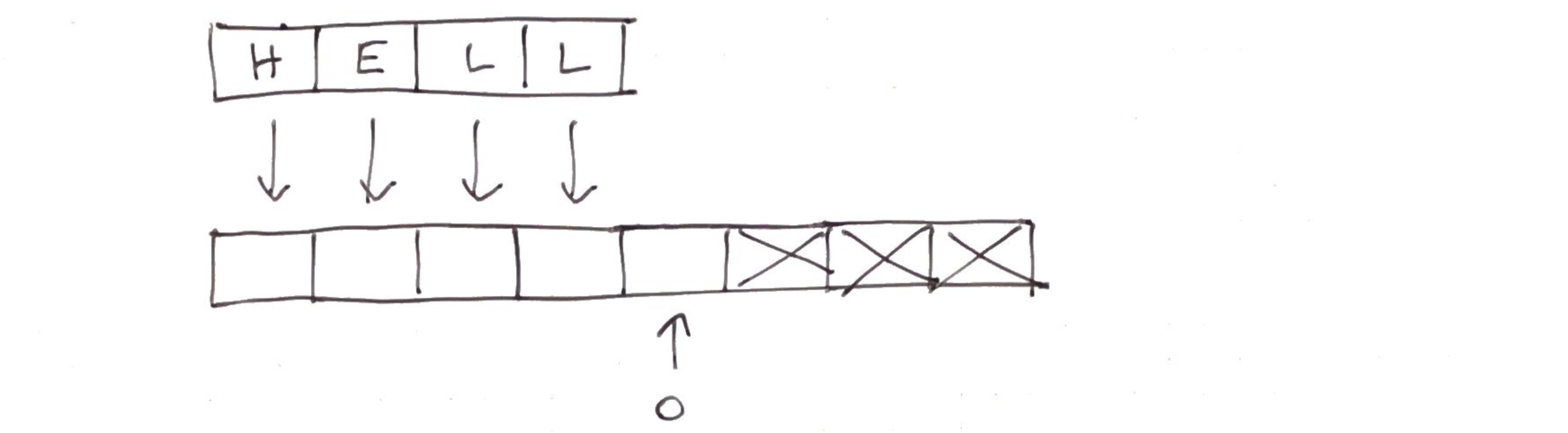
L'insertion sans changement de capacité est simplement

Tandis que celle avec changement de capacité devient
T = Tableau()
print(T)
for i in range(9):
inserer_en_queue(T,i*i)
print(T)
T(0/0): [] T(1/1): [0] T(2/2): [0, 1] T(3/4): [0, 1, 4, None] T(4/4): [0, 1, 4, 9] T(5/8): [0, 1, 4, 9, 16, None, None, None] T(6/8): [0, 1, 4, 9, 16, 25, None, None] T(7/8): [0, 1, 4, 9, 16, 25, 36, None] T(8/8): [0, 1, 4, 9, 16, 25, 36, 49] T(9/16): [0, 1, 4, 9, 16, 25, 36, 49, 64, None, None, None, None, None, None, None]
Insérer en position¶
La seule différence avec l'insertion en queue est qu'il faut déplacer les éléments d'incides [indice,taille[ de 1 vers la droite avant d'écrire à l'indice demandé.
Lors des réallocations, le déplacement s'effectue en une seule fois de data à tmp et de 1 position vers la droite.
def inserer_en_position(T,i,valeur):
if T.taille >= T.capacite:
T.capacite = 2 * T.capacite if T.capacite > 0 else 1
tmp = [None]*T.capacite
tmp[0:i] = T.data[0:i]
tmp[T.taille:i:-1] = T.data[T.taille-1:i-1:-1]
T.data = tmp
else:
T.data[T.taille:i:-1] = T.data[T.taille-1:i-1:-1]
T.data[i] = valeur
T.taille += 1
L'insertion sans changement de capacité est simplement
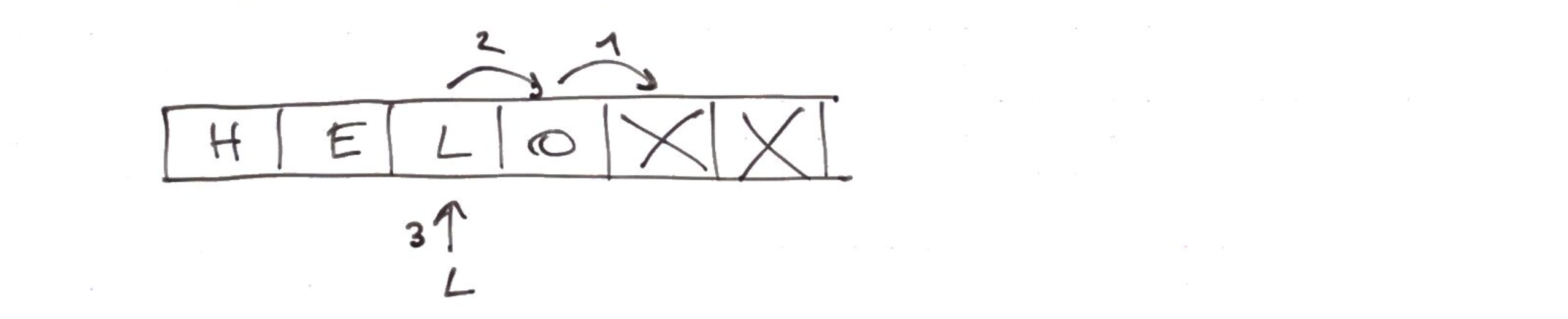
Tandis que celle avec changement de capacité devient
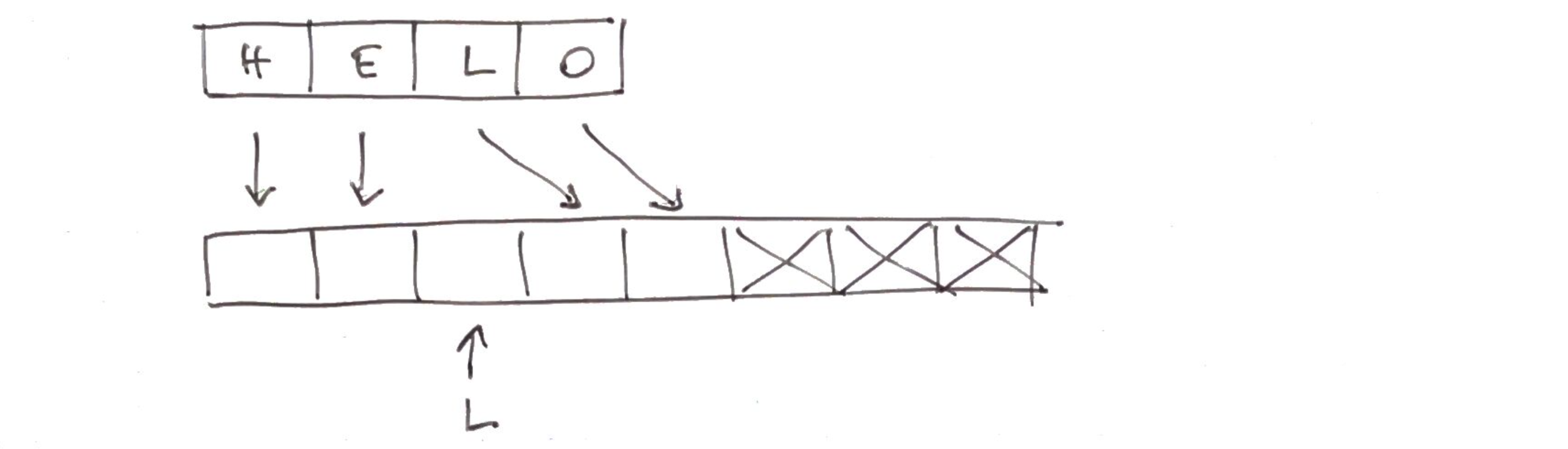
T = Tableau()
print(T)
for i in range(9):
pos = ( len(T) + 1 )// 2
inserer_en_position(T,pos,i*i)
print(pos,T)
T(0/0): [] 0 T(1/1): [0] 1 T(2/2): [0, 1] 1 T(3/4): [0, 4, 1, None] 2 T(4/4): [0, 4, 9, 1] 2 T(5/8): [0, 4, 16, 9, 1, None, None, None] 3 T(6/8): [0, 4, 16, 25, 9, 1, None, None] 3 T(7/8): [0, 4, 16, 36, 25, 9, 1, None] 4 T(8/8): [0, 4, 16, 36, 49, 25, 9, 1] 4 T(9/16): [0, 4, 16, 36, 64, 49, 25, 9, 1, None, None, None, None, None, None, None]
Redimensionner¶
Redimensionner utilise le même code de réallocation que d'insérer en queue. Ensuite, on ajoute les nouveau éléments ou en détruit les anciens selon que la taille augmente ou diminue.
def redimensionner(T,taille_demandee,valeur = 0):
diff = taille_demandee - T.taille
if taille_demandee >= T.capacite:
T.capacite = taille_demandee
tmp = [None]*T.capacite
tmp[0:T.taille] = T.data[0:T.taille]
T.data = tmp
if diff > 0:
T.data[T.taille:taille_demandee] = [valeur]*diff
else:
T.data[taille_demandee:T.taille] = [None]*-diff
T.taille = taille_demandee
T = Tableau()
for i in range(5): inserer_en_queue(T,i)
print(T)
redimensionner(T,3)
print(T)
redimensionner(T,6,42)
print(T)
redimensionner(T,11,-1)
print(T)
T(5/8): [0, 1, 2, 3, 4, None, None, None] T(3/8): [0, 1, 2, None, None, None, None, None] T(6/8): [0, 1, 2, 42, 42, 42, None, None] T(11/11): [0, 1, 2, 42, 42, 42, -1, -1, -1, -1, -1]
Faut-il diminuer la capacité?¶
Pas vraiment.
En C++, la STL
- ne le fait pas automatiquement
- ne fournit
std::vector::shrink_to_fit()que depuis C++11.
Si on veut le faire automatiquement, il faut choisir un critère différent de celui d'augmentation. Par exemple
- multiplier par deux la capacité si
taille >= capacite - diviser par deux la capacité si
taille < capacite / 4
Complexité¶
Pour mesurer la complexité de l'opération d'insertion en queue avec réallocation en cas de capacité insuffisante, comptons les écritures dans les tableaux.
def inserer_en_queue_cnt(T,valeur):
cnt = 0
if T.taille >= T.capacite:
T.capacite = 2 * T.capacite if T.capacite > 0 else 1
tmp = [None]*T.capacite
tmp[0:T.taille] = T.data[0:T.taille]; cnt += T.taille
T.data = tmp
T.data[T.taille] = valeur; cnt += 1
T.taille += 1
return cnt
Intéressons nous au remplissage d'un tableau originellement vide en appelant $n$ fois inserer_en_queue
T = Tableau();
for i in range(n): inserer_en_queue(T,i*i)
La complexité de l'insertion de $n$ semble linéaire en $n$
import include.tableau_capacite_variable as ext
ext.affiche_complexite_1(Tableau,inserer_en_queue_cnt)
<Figure size 640x480 with 1 Axes>
Un graphique linéraire nous donne une meilleure vue. Les nombre d'écritures varie entre 2 et 3 fois la taille.
ext.affiche_complexite_2(Tableau,inserer_en_queue_cnt)
La complexité d'une seule opération d'insertion est la plupart du temps $\Theta(1)$. Il n'y a pas de redimensionnement, ce qui est le meilleur cas.
Elle est $\Theta(n)$ quand on doit augmenter la capacité, i.e. pour $n = 2^k+1$ avec $k$ entier, les pires cas.
ext.affiche_complexite_3(Tableau,inserer_en_queue_cnt)
En moyenne, la complexité de inserer_en_queue est constante $\Theta(1)$.
ext.affiche_complexite_4(Tableau,inserer_en_queue_cnt)

|
© Olivier Cuisenaire, 2018 |