Tri de listes¶

Principe¶

Les algorithmes vu au chapitre 3 ne sont pas directement applicables aux listes simplement ou doublement chainées

Il n'y a pas d'accès indexé aux éléments

Le fournir serait trop cher en terme de complexité

Mais en a-t-on vraiment besoin ?

Cela dépend des algorithmes

Tri à bulle et par sélection¶

Pour rappel, en voici les codes du chapitre 3 pour trier des tableaux

In [1]:

def tri_a_bulles(T):
    N = len(T)
    for k in range(N,1,-1):    
        for i in range(0,k-1):  
            if T[i] > T[i+1]: 
                T[i],T[i+1] = T[i+1],T[i]

In [2]:

def tri_par_selection(T):
    N = len(T)
    for i in range(0,N-1):
        jMin = i
        for j in range(i+1,N):
            if T[j] < T[jMin]: jMin = j
        T[i],T[jMin] = T[jMin],T[i]

Dans les deux cas, il y a

deux parcours croissants
des échanges d'éléments

Les parcours croissants peuvent aisément être effectués par les itérateurs sur listes simples ou doubles. Par exemple, pour le tri par sélection

In [3]:

def tri_par_selection(L):
    i = L.begin()
    while i != L.end():
        jMin = i.copie()
        j = i.suivant(); 
        while j != L.end():
            if j.get_val() < jMin.get_val():
                jMin = j.copie()
            j.incr()
        echanger(i,jMin)
        i.incr()

Avec une fonction d'échange standard entre les éléments itérés, on a

In [4]:

def echanger(i,j):
    tmp = i.get_val()
    i.set_val(j.get_val())
    j.set_val(tmp)

In [5]:

import include.liste_double as ld
def liste_demo():
    T = [ 6, 3, 5, 4, 1, 2, 8, 7, 9 ]; 
    L = ld.Liste()
    for t in T: 
        L.push_back(t)
    return L

In [6]:

L = liste_demo();     print(L); 
tri_par_selection(L); print(L)

6 ⇄ 3 ⇄ 5 ⇄ 4 ⇄ 1 ⇄ 2 ⇄ 8 ⇄ 7 ⇄ 9
1 ⇄ 2 ⇄ 3 ⇄ 4 ⇄ 5 ⇄ 6 ⇄ 7 ⇄ 8 ⇄ 9

Mais il y a une autre manière d'échanger les éléments sans devoir les copier: échanger la place de leurs maillons dans la chaine.

Considérons la liste suivante dont on veut échanger les maillons 2 et 5

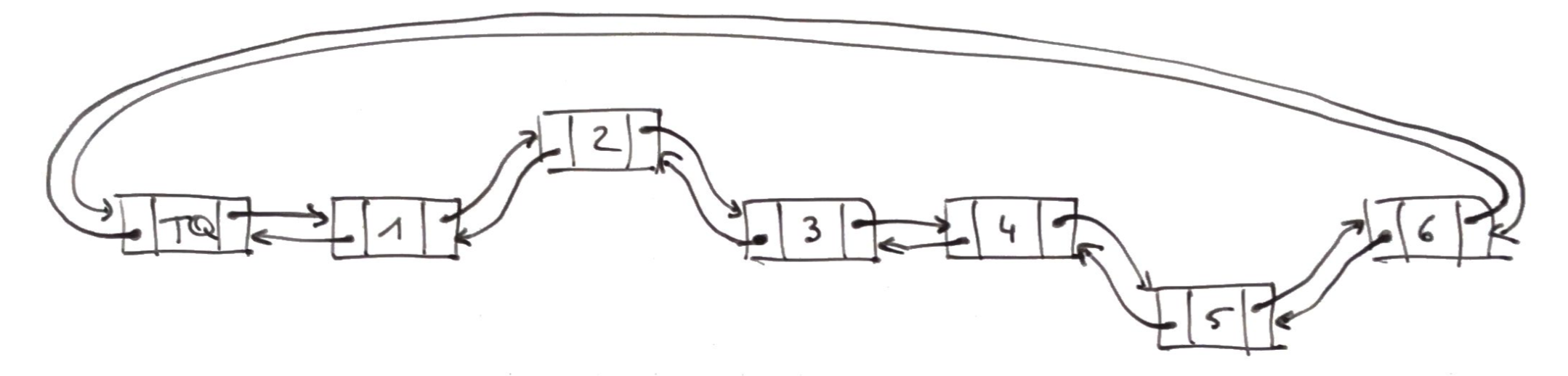
Il va falloir modifier les liens colorés.

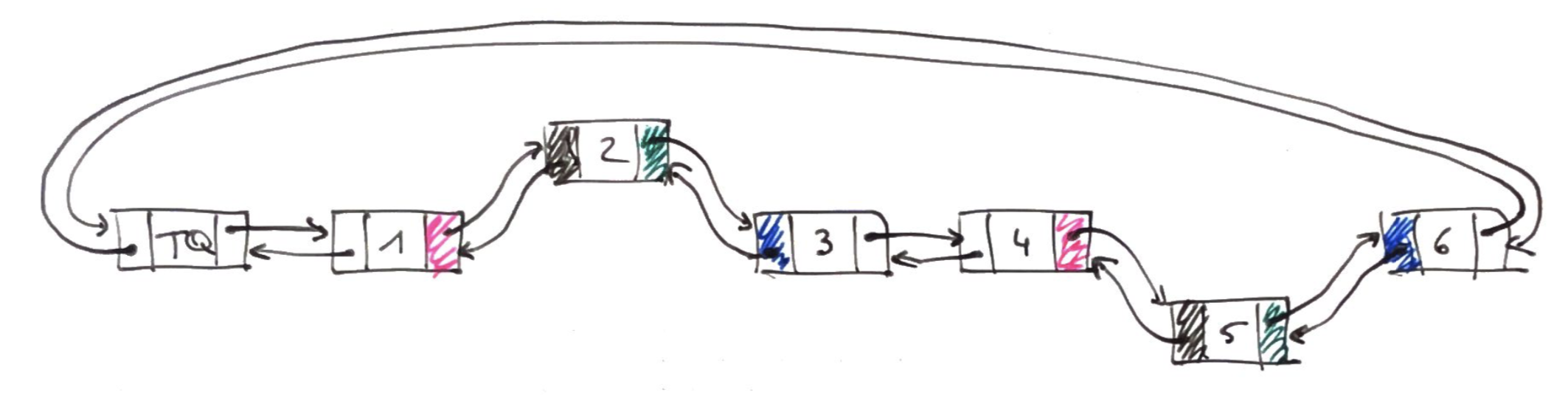
Les couleurs font correspondre les liens équivalents pour chacun des maillons à échanger

rose: m.precedent.suivant
noir: m.precedent
vert: m.suivant
bleu: m.suivant.precedent

Il suffit d'échanger ces liens correspondant 2 par 2 pour obtenir la liste modifiée.

On procède en deux étapes.

indentifier m1p, m1s, m2p, m2s, les noeuds entourant m1 et m2
effectuer les 4 échanges de liens équivalents

In [7]:

def echanger_emplacement_des_maillons(m1,m2):
    if m1 == m2: return
    
    m1p = m1.precedent; m1s = m1.suivant
    m2p = m2.precedent; m2s = m2.suivant
    
    m1p.suivant, m2p.suivant = m2p.suivant, m1p.suivant
    m1.suivant, m2.suivant = m2.suivant, m1.suivant
    
    m1s.precedent, m2s.precedent = m2s.precedent, m1s.precedent
    m1.precedent, m2.precedent = m2.precedent, m1.precedent 
    
def echanger_iterateurs(i,j):
    if i == j: return 
    echanger_emplacement_des_maillons(i._list_iterator__M, 
                                      j._list_iterator__M)

Mais attention, après échange, les itérateurs pointent toujours sur les mêmes éléments, mais ne sont plus au même emplacement de la liste

In [8]:

L = liste_demo()
i = L.begin().suivant(0)
j = L.begin().suivant(4)
print(i,j,L)

echanger_iterateurs(i,j)
print(i,j,L)

6 1 6 ⇄ 3 ⇄ 5 ⇄ 4 ⇄ 1 ⇄ 2 ⇄ 8 ⇄ 7 ⇄ 9
6 1 1 ⇄ 3 ⇄ 5 ⇄ 4 ⇄ 6 ⇄ 2 ⇄ 8 ⇄ 7 ⇄ 9

Après échange des maillons, c'est jMin qui stocke maintenant l'emplacement dans la boucle sur i

In [9]:

def tri_par_selection(L):
    i = L.begin()
    while i != L.end():
        jMin = i.copie()
        
        j = i.suivant(); 
        while j != L.end():
            if j.get_val() < jMin.get_val():
                jMin = j.copie()
            j.incr()
            
        echanger_iterateurs(i,jMin)
        i = jMin.suivant()    # et pas i.incr()

In [10]:

L = liste_demo();     print(L); 
tri_par_selection(L); print(L)

6 ⇄ 3 ⇄ 5 ⇄ 4 ⇄ 1 ⇄ 2 ⇄ 8 ⇄ 7 ⇄ 9
1 ⇄ 2 ⇄ 3 ⇄ 4 ⇄ 5 ⇄ 6 ⇄ 7 ⇄ 8 ⇄ 9

Tri par insertion¶

Nous avons déjà vu la traduction du tri par insertion en itérateurs dans la section sur les listes

In [11]:

def tri_par_insertion(L):
    if L.size() < 2: return
    
    k = L.begin().suivant()
    while k != L.end():
        tmp = k.get_val()
        
        j = k; i = j.precedent()
        while j != L.begin() and tmp < i.get_val():
            j.set_val(i.get_val())
            j = i.copie() 
            i.decr()
            
        j.set_val(tmp)
        k.incr()

Ce code est une transcription exacte de celui sur les tableaux. Mais ce n'est pas efficace.

Le but de la boucle interne est de

trouver la position i où il faut insérer l'élément k
déplacer l'élément de k vers i

Dans un tableau, cela requiert de déplacer tous les éléments entre i et k-1 de 1 vers la droite. Mais dans une liste chainée, cela n'a pas de sens. Il suffit de retirer le maillon k et de l'insérer tel quel devant i,

Soit la liste suivante dont nous voulons insérer le maillon 2 devant le maillon 3

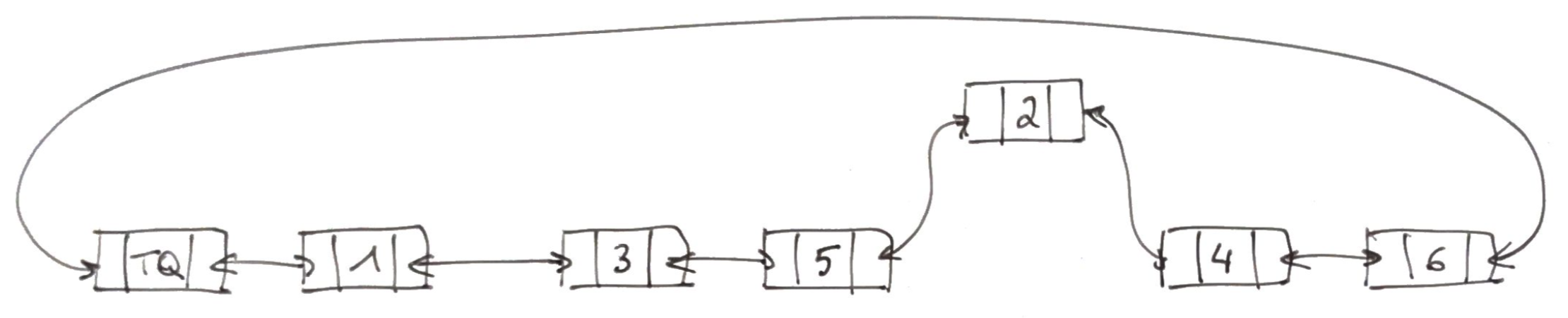
Il suffit de détruire les liens pointillés et d'écrire à la places les liens doubles bleu, vert et rose.

In [13]:

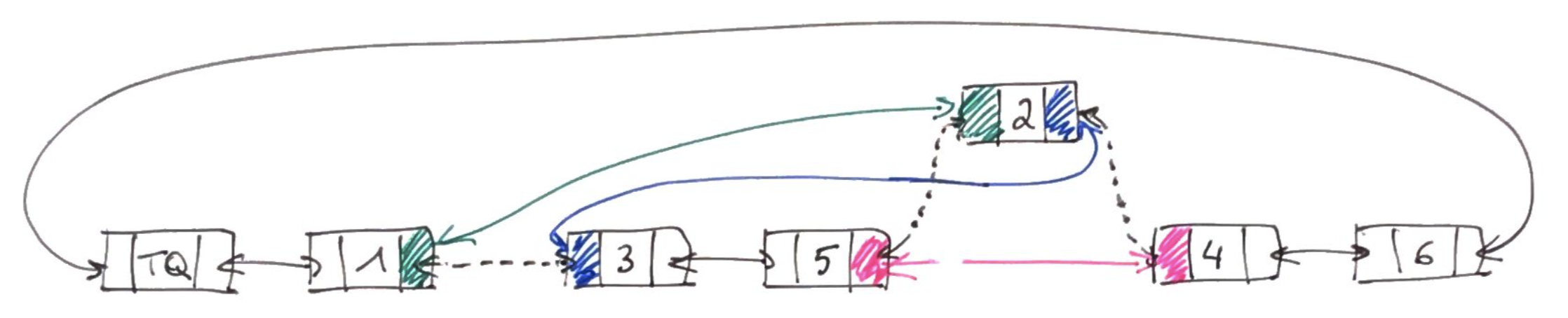
def deplacer_maillon(FROM,TO):
    if FROM == TO: return

    # rose 
    FROM.precedent.suivant = FROM.suivant    
    FROM.suivant.precedent = FROM.precedent
    
    # vert
    TO.precedent.suivant = FROM
    FROM.precedent = TO.precedent
    
    # bleu
    TO.precedent = FROM
    FROM.suivant = TO

In [14]:

def deplacer_iterateur(FROM,TO):
    deplacer_maillon(FROM._list_iterator__M,
                     TO._list_iterator__M)

Elle nous permet de ré-écrire le tri par insertion

In [15]:

def tri_par_insertion(L):
    if L.size() < 2: return
    
    k = L.begin().suivant()
    while k != L.end():    
        i = k.copie()
        while i != L.begin() and \
              k.get_val() < i.precedent().get_val():
            i.decr()
        n = k.suivant()
        deplacer_iterateur(k,i)
        k = n

In [16]:

L = liste_demo();     print(L)
tri_par_insertion(L); print(L)

6 ⇄ 3 ⇄ 5 ⇄ 4 ⇄ 1 ⇄ 2 ⇄ 8 ⇄ 7 ⇄ 9
1 ⇄ 2 ⇄ 3 ⇄ 4 ⇄ 5 ⇄ 6 ⇄ 7 ⇄ 8 ⇄ 9

Episser (to splice)¶

On peut généraliser l'opération de déplacement de maillons en déplaçant toute une sous-liste à un autre emplacement, voire à un emplacement d'un autre liste.

Cette opération s'appelle l'épissure, splice en anglais. C'est un mot du vocabulaire marin, provenant etymologiquement du néerlandais splitsen: assembler deux cordes ou deux câbles mis bout à bout par l’entrelacement de leurs torons.

Le code est assez similaire à celui du déplacement d'un noeud. Il faut modifier 3 liens doubles, soit 6 liens.

Pour insérer la sous-liste [debut2,fin2[ devant le maillon m1, il faut supprimer les doubles liens pointillés et les remplacer par les doubles liens rose, vert, et bleu

In [17]:

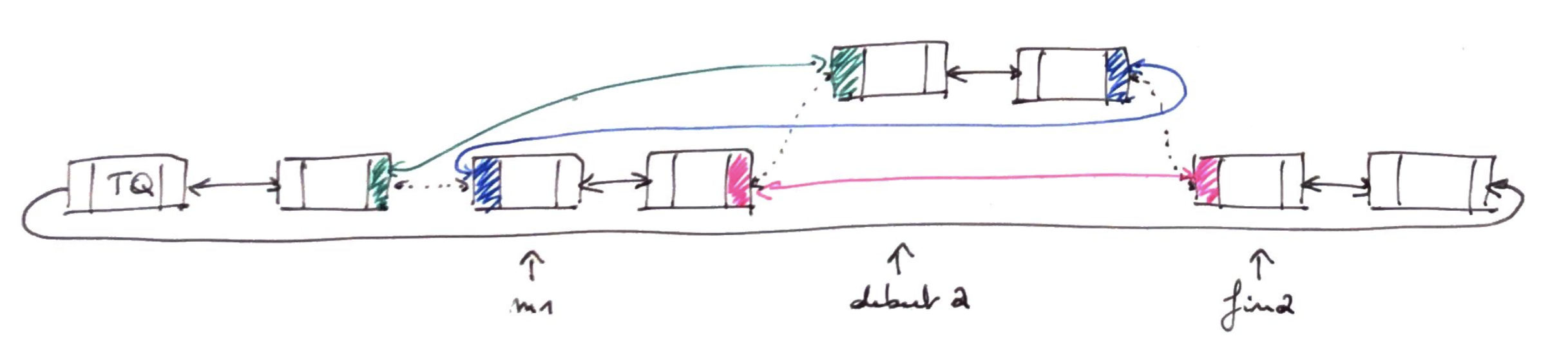
def splice_maillons(m1,debut2,fin2):
    if debut2 == fin2: return    # rien à épisser
    
    m1p = m1.precedent 
    d2p = debut2.precedent
    f2p = fin2.precedent 
        
    # rose 
    d2p.suivant = fin2; fin2.precedent = d2p

    # vert
    m1p.suivant = debut2; debut2.precedent = m1p

    # bleu
    f2p.suivant = m1; m1.precedent = f2p

Si l'on permet de transférer des maillons d'une liste à l'autre, on ne peut pas se contenter d'une API basée sur les itérateurs. L'épissure modifie le nombre d'éléments des deux listes

In [18]:

def splice(it1,begin2,end2, L1 = None, L2 = None):
    if L1 != L2 and L1 and L2: 
        n = distance(begin2,end2)
        L1._Liste__N += n; L2._Liste__N -= n

    splice_maillons(it1._list_iterator__M,
                   begin2._list_iterator__M,
                   end2._list_iterator__M)

In [19]:

def distance(it1,it2):
    cnt = 0; it = it1.copie()
    while it != it2:
        it.incr()
        cnt += 1
    return cnt

In [20]:

L1 = ld.Liste()
for i in range(-1,-7,-1): L1.push_back(i)
print(L1)

-1 ⇄ -2 ⇄ -3 ⇄ -4 ⇄ -5 ⇄ -6

In [21]:

L2 = ld.Liste()
for i in range(7): L2.push_back(i)
print(L2)

0 ⇄ 1 ⇄ 2 ⇄ 3 ⇄ 4 ⇄ 5 ⇄ 6

In [22]:

i1 = L1.begin().suivant(2)
b2 = L2.begin().suivant(1)
e2 = L2.begin().suivant(4)
splice(i1,b2,e2,L1,L2)

In [23]:

print(L1.size(),": ",L1)
print(L2.size(),": ",L2)

9 :  -1 ⇄ -2 ⇄ 1 ⇄ 2 ⇄ 3 ⇄ -3 ⇄ -4 ⇄ -5 ⇄ -6
4 :  0 ⇄ 4 ⇄ 5 ⇄ 6

Tri fusion¶

La fonction récursive du tri fusion ne pose pas de problème dès lors que toutes les opérations

tri fusion récursif
fonction de fusion

retournent les itérateurs de début et de fin de la sous-liste ainsi triée.

In [24]:

def tri_fusion_rec(begin,n):
    if n > 1:
        b1,e1 = tri_fusion_rec(begin,n//2)
        b2,e2 = tri_fusion_rec(e1,n - n//2)
        return fusion(b1,b2,e2)
    else: # n == 1
        return begin, begin.suivant()
    
def tri_fusion(L):
    tri_fusion_rec(L.begin(),L.size())

La fonction de fusion peut être mise en oeuvre au moyen de la fonction splice. Elle ne requiert pas de copie d'éléments et a donc une complexité spatiale constante.

In [25]:

def fusion(begin, mid, end):
    before_begin = begin.precedent()
    
    L1 = ld.Liste(); splice(L1.end(),begin,mid); 
    L2 = ld.Liste(); splice(L2.end(),mid,end);   
    it1 = L1.begin(); it2 = L2.begin()
    
    while not (L1.empty() and L2.empty()):
        if L2.empty(): it1 = L1.end()
        else: 
            while it1 != L1.end() and \
                  not it2.get_val() < it1.get_val(): 
                it1.incr()
        splice(end,L1.begin(),it1)

        if L1.empty(): it2 = L2.end()
        else:
            while it2 != L2.end() and \
                  it2.get_val() < it1.get_val():     
                it2.incr()
        splice(end,L2.begin(),it2)

    return before_begin.suivant(), end

Tri rapide¶

La mise en oeuvre de l'algorithme de partition ne pose pas de problème particulier pour une liste doublement chainée, toutes les opérations étant disponibles.

Par contre, elle doit retourner non plus un seul indice, mais tous les itérateurs nécessaires aux appels récursifs qui suivent.

Si ces itérateurs sont bien retournés, la mise en oeuvre de la fonction doublement récursive ne pose pas non plus problème.

Le choix du pivot est problématique puisqu'il requiert éventuellement un parcours partiel selon l'algorithme de choix sélectionné

Il est possible de trier une liste simplement chainée, mais cela requiert de modifier l'algorithmne de partition

En pratique, on utilise plutôt le tri fusion.

Tri par tas, tri de Shell¶

ces tris ont intrinsèquement besoin d'un accés aléatoire aux données. Ils ne peuvent être mis en oeuvre efficacement sur des listes chainées.

ASD1 Notebooks on GitHub.io