Arbres binaires de recherche en C++

La Standard Template Library utilise les arbres binaires de recherche pour mettre en oeuvre les conteneurs associatifs suivants

Conteneur	Description
std::set	Ensemble trié d'éléments uniques
std::multiset	Ensemble trié d'éléments pouvant être présents plusieurs fois
std::map	Tableau associatif utiliant des clés triées uniques associées à des valeurs
std::multimap	Tableau associatif utiliant des clés triées non-uniques associées à des valeurs

Dans tous les cas, les éléments / clés doivent être comparables, soit par l'opérateur <, soit par une fonction de comparaison fournie explicitement à la construction.

Depuis C++11, ces quatre conteneurs précédés de unordered_ fournissent les même fonctionnalités - mais sans trier le contenu - au moyen de tables de hachage (cfr. ASD2)

• std::unordered_set

• std::unordered_multiset

• std::unordered_map

• std::unordered_multimap

Il n'est pas nécessaire que les éléments soient comparables.

La STL fournit aussi des fonctions de la librairie <algorithm> mettant en oeuvre la théorie des ensembles de Cantor.

Fonction	Description
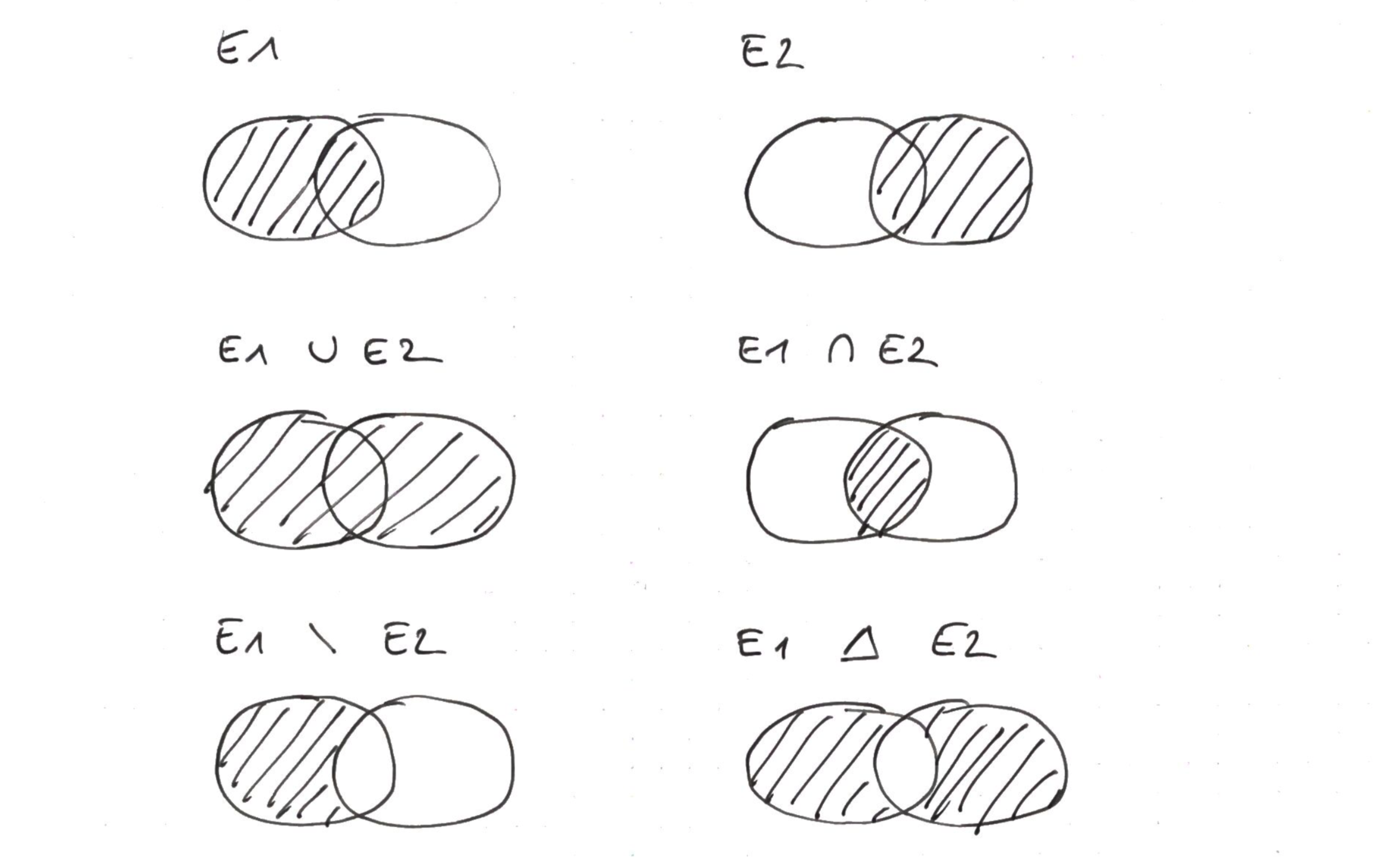
std::set_union	$A \cup B = \{ x : x \in A \lor x \in B \}$
std::set_intersection	$A \cap B = \{ x : x \in A \land x \in B \}$
std::set_difference	$A \setminus B = \{ x : x \in A \land x \notin B \}$
std::set_symmetric_difference	$A \triangle B = (A \cup B) \setminus (A \cap B)$

ces fonctions ont besoin d'entrées triées, et ne fonctionnent donc pas avec le conteneur unordered_set.

std::set

met en oeuvre le TDA ensemble. Les éléments ne peuvent être modifiés, mais seulement insérés ou supprimés. Les opérations sont

Opération	Méthode(s) set::...
Insertion	insert, emplace, emplace_hint
Construction	set
Suppression	erase
Recherche	find, lower_bound, upper_bound
Itération ordonnée	(c)(r)begin, (c)(r)end

Il est typiquement mis en oeuvre au moyen d'un arbre rouge-noir (ABR équilibré, voir ASD2)

L'insertion d'un élément peut se faire selon deux méthodes

pair<iterator,bool> set::insert (const value_type& val);

• recherche l'élément en $\Theta( \log n)$,

• l'insère s'il est absent,

• retourne pair<iterator,bool> dont le second terme indique s'il y a eu insertion,

• et le premier élément est un itérateur vers l'élément trouvé ou inséré.

pair<iterator,bool> set::insert (const_iterator position, 
                                 const value_type& val);

• utilise l'itérateur position comme indice,

• a une complexité moyenne $\Theta(1)$ si l'indice itère sur l'élément
  • qui suivra val dans le set (C++11 et suivants)
  • qui précédera val dans le set (C++98)

Il est également possible d'insérer plusieurs éléments à la fois

std::set dispose des constructeurs habituels

• par défaut
• par déplacement
• par copie
• depuis une séquence d'éléments ou une liste d'initialisation

Les deux premiers sont de complexité constante $\Theta(1)$.

Les autres sont de complexité

• $\Theta(n)$, i.e. linéaire si les éléments à insérer sont triés
• donc linéaire pour le constructeur de copie
• $\Theta(n \log n)$ , i.e. linéarithmique sinon

La suppression se fait au moyen de la méthode erase. Sa complexité dépend de l'argument fourni en entrée

Argument	Complexité
un itérateur	$\Theta(1)$, constante en moyenne
une valeur	$\Theta(\log n)$, logarithmique
une plage [first,last[	$\Theta(d)$, linéaire en la distance $d$ entre first et last

La recherche peut se faire via trois méthodes.

Méthode	Retourne
find(val)	un itérateur vers l'élément trouvé, set::end() sinon
lower_bound(val)	un itérateur vers le premier élément plus grand ou égal à val
upper_bound(val)	un itérateur vers le premier élément strictement plus grand que val

Toutes ces recherches se font en temps logarithmique $\Theta(n)$

Enfin, il propose des itérateurs bi-directionnels parcourant l'ensemble trié. Les 4 versions sont disponibles

• begin() → end()
• cbegin() → cend()
• rbegin() → rend()
• crbegin() → crend()

Parcourir tout l'arbre avec ces itérateurs à une complexité linéaire $\Theta(n)$ pour $n$ éléments.

La complexité d'un operator++ est en moyenne $\Theta(1)$, mais au pire $\Theta(\log n)$.

Ces itérateurs n'offrent pas d'accès aléatoire, la STL ayant choisi de ne pas stocker d'attibut taille en chaque noeud.

// Exemple d'utilisation de std::set
#include <set>
using namespace std; 

string hello = "bonjour le monde";
set<char> s;                       // constructeur par défaut
for(char c : hello) s.insert(c);   // insertion
for(char c : s) cout << c;         // parcours ordonné

 bdejlmnoru

set<char> s2(hello.begin(),hello.end()); // construction en 
       // O(n log m) avec n = hello.size() et m = s2.size()

for(char c : s2) cout << c;             // parcours ordonné

 bdejlmnoru

set<char> s3(s.begin(),s.end());  // construction en 
        // O(n) depuis une plage triée de n éléments 

for(char c : s3) cout << c;       // parcours ordonné

 bdejlmnoru

s2.erase(next(s2.begin()));  // suppression du deuxième élément

for(char c : s2) cout << c;  // parcours ordonné

 dejlmnoru

s2.erase('m');               // suppression de l'élément 'm'

for(char c : s2) cout << c;  // parcours ordonné

 dejlnoru

s2.erase(s2.lower_bound('e'), s2.upper_bound('o'));
                // lower_bound: recherche de 'e' ou plus grand
                // upper_bound: recherche de plus grand que 'o'
                // erase: suppression d'une plage d'éléments

for(char c : s2) cout << c;                // parcours ordonné

 dru

std::map<Key,Value>

met en oeuvre le TDA tableau associatif dont les clés sont uniques. Une map est essentiellement un set dont les éléments sont de type std::pair<const Key, Value>, et dont la fonction de comparaison n'utilise que la clé et pas la valeur

template <typename K, typename V>
bool compare(const pair<const K,V>& a, 
             const pair<const K,V>& b) 
{
    return a.first < b.first; 
}

On peut en gérer le contenu via des méthodes similaires à celles de set et ces paires, mais il est plus pratique de ce servir de map<K,T>::operator[].

L'opérateur crochet a comme prototype

V& map<K,T>::operator[](const K& k)

Il reçoit une clé en paramètre et retourne une référence à la valeur associée.

Selon la documentation, il est équivalent à

(*((this->insert(make_pair(k,V()))).first)).second

Décomposons cette expression pour la comprendre.

// (*((this->insert(make_pair(k,V()))).first)).second

template <typename K, typename V> 
V& map<K,V>::operator[](const K& k) 
{
    V                             v = V();
    
    pair<K,V>                     p = make_pair(k,v);
    
    pair<map<K,V>::iterator,bool> r = this->insert(p);
    
    map<K,V>::iterator            i = r.first;
    
    pair<K,V>&                    q = *i;
    
    V&                            w = q.second;
    
    return w; 
}

Il y a deux cas possibles selon que la clé k est déjà présente ou pas dans la map m.

• si k est absente, l'expression m[k] insère la paire make_pair(k,V()) qui associe la valeur par défaut V() à la clé k.

• si k est présente, l'expression m[k] n'insère rien

Dans les deux cas, elle retourne une référence à la valeur associée à k, ce qui permet de la modifier par affectation, i.e. m[k] = v;

Attention, l'expression cout << m[k]; modifie la map m en y ajoutant make_pair(k,V()) si k était absent.

// Exemple d'utilisation

#include <map>

hello = "abracadabra";
std::map<char,size_t> m;

size_t i = 0;
for(char c : hello)
    m[c] = i++;

for(auto p : m)
    cout << "m[" << p.first << "]=" << p.second << "\n";

m[a]=10
m[b]=8
m[c]=4
m[d]=6
m[r]=9

// Attention, cout << m[c] modifie m si la clé était absente

cout << m.size() << "\n"; 

for(char c = 'c'; c <= 'e'; ++c)
    cout << "m[" << c << "]=" << m[c] << "\n";

cout << m.size() << "\n";

5
m[c]=4
m[d]=6
m[e]=0
6

// On peut l'éviter en utilisant la fonction find.

std::cout << m.size() << "\n"; 

for(char c = 'd'; c <= 'f'; ++c) 
{ 
    auto it = m.find(c);
    if(it != m.end())
        std::cout << "m[" << c << "]=" << (*it).second << "\n";
    else 
        std::cout << "m[" << c << "] est absent\n";
}

std::cout << m.size() << "\n";

6
m[d]=6
m[e]=0
m[f] est absent
6

std::multiset et std::multimap

offrent essentiellement les mêmes méthodes que std::set et std::map mais permettent de stocker plusieurs fois la même clé.

Dès lors, std::multimap n'offre pas d'operator[] qui serait équivoque.

Ils fournissent tous deux une méthode equal_range qui retourne la plage de tous les éléments de clés équivalentes. Son implantation utilise lower_bound et upper_bound

template <typename T>
pair<multiset<T>::iterator,multiset<T>::iterator> 
multiset<T>::equal_range (const T& k) 
{
    return make_pair(lower_bound(k),upper_bound(k));
}

Opérations sur les ensembles

Les fonctions set_union, set_intersection, set_difference, et set_symmetric_difference de la librairie <algorithm>

• prennent en entrée des plages d'éléments triés
• écrivent le résultat trié dans un itérateur de sortie
• retournent l'itérateur suivant le dernier élément écrit.

Leur prototype commun est

template <class InputIterator1, class InputIterator2,
          class OutputIterator>
OutputIterator set_xxx (
    InputIterator1 first1, InputIterator1 last1,
    InputIterator2 first2, InputIterator2 last2,
    OutputIterator result);

Ces fonctions sont équivalentes aux codes génériques suivants

template <class InputIter1, class InputIter2,
          class OutputIter>
OutputIter set_union (
              InputIter1 first1, InputIter1 last1,
              InputIter2 first2, InputIter2 last2,
              OutputIter result)
{
  while (true)
  {
    if (first1==last1) return std::copy(first2,last2,result);
    if (first2==last2) return std::copy(first1,last1,result);

    if (*first1<*first2) { *result = *first1; ++first1; }
    else if (*first2<*first1) { *result = *first2; ++first2; }
    else { *result = *first1; ++first1; ++first2; }
    ++result;
  }
}

template <class InputIter1, class InputIter2,
          class OutputIter>
OutputIter set_intersection (
              InputIter1 first1, InputIter1 last1,
              InputIter2 first2, InputIter2 last2,
              OutputIter result)
{
  while (first1!=last1 && first2!=last2)
  {
    if (*first1<*first2) ++first1;
    else if (*first2<*first1) ++first2;
    else {
      *result = *first1;
      ++result; ++first1; ++first2;
    }
  }
  return result;
}

template <class InputIter1, class InputIter2,
          class OutputIter>
OutputIter set_difference (
              InputIter1 first1, InputIter1 last1,
              InputIter2 first2, InputIter2 last2,
              OutputIter result)
{
  while (first1!=last1 && first2!=last2)
  {
    if (*first1<*first2) { 
        *result = *first1; ++result; ++first1; 
    }
    else if (*first2<*first1) ++first2;
    else { ++first1; ++first2; }
  }
  return std::copy(first1,last1,result);
}

template <class InputIter1, class InputIter2,
          class OutputIter>
OutputIter set_symmetric_difference (
              InputIter1 first1, InputIter1 last1,
              InputIter2 first2, InputIter2 last2,
              OutputIter result)
{
  while (true)
  {
    if (first1==last1) return std::copy(first2,last2,result);
    if (first2==last2) return std::copy(first1,last1,result);

    if (*first1<*first2) { 
        *result=*first1; ++result; ++first1; 
    }
    else if (*first2<*first1) { 
        *result = *first2; ++result; ++first2; 
    }
    else { ++first1; ++first2; }
  }
}

Dans tous les cas, les deux entrées doivent être triées et sans doublons. C'est le cas si l'on utilise des std::set, mais on peut aussi utiliser une autre structure que l'on trie et dont on supprime les doublons

#include <set>
set<int> E1 = { 5, 10, 15, 20, 25, 5, 10}; 

cout << "E1:  " << str(E1) << "\n";

E1:  [ 5, 10, 15, 20, 25]

#include <list>
list<int> E2 = { 50, 40, 10, 20, 30, 10, 40 };
E2.sort();
E2.unique();

cout << "E2:  " << str(E2) << "\n";

E2:  [ 10, 20, 30, 40, 50]

#include <forward_list>
forward_list<int> E3 = { 5, 10, 15, 20, 25, 5, 10}; 
E3.sort();
E3.unique();

cout << "E3:  " << str(E3) << "\n";

E3:  [ 5, 10, 15, 20, 25]

#include <vector>
#include <algorithm>
vector<int> E4 = { 50, 40, 10, 20, 30, 10, 40 };
sort(E4.begin(),E4.end());
auto last = unique(E4.begin(),E4.end());
E4.erase(last,E4.end());

cout << "E4:  " << str(E4) << "\n";

E4:  [ 10, 20, 30, 40, 50]

Pour la sortie, il faut fournir un emplacement où écrire les résultats. Une solution consiste à écrire dans une structure linéaire de taille suffisante, puis à supprimer les emplacements excédentaires

vector<int> U(E1.size()+E2.size());

auto lastU = std::set_union(E1.begin(), E1.end(), 
                          E2.begin(), E2.end(), 
                          U.begin());
U.erase(lastU,U.end());

cout << "E1: " << str(E1) << "\n";
cout << "E2: " << str(E2) << "\n";
cout << "U:  " << str(U) << "\n";

E1: [ 5, 10, 15, 20, 25]
E2: [ 10, 20, 30, 40, 50]
U:  [ 5, 10, 15, 20, 25, 30, 40, 50]

Une autre approche consiste à utiliser une structure linéaire offrant la méthode push_back, en combinaison avec un std::back_inserter

#include <iterator>

list<int> I;
std::set_intersection(E1.begin(), E1.end(), 
                     E2.begin(), E2.end(), 
                     back_inserter(I));

cout << "E1: " << str(E1) << "\n";
cout << "E2: " << str(E2) << "\n";
cout << "I:  " << str(I) << "\n";

E1: [ 5, 10, 15, 20, 25]
E2: [ 10, 20, 30, 40, 50]
I:  [ 10, 20]

Il est même possible d'utiliser un std::front_inserter en combinaison avec structure offrant la méthode push_front, mais il faut inverser le résultat

forward_list<int> D;
std::set_difference(E1.begin(), E1.end(), 
                    E2.begin(), E2.end(), 
                    front_inserter(D));
D.reverse();

cout << "E1: " << str(E1) << "\n";
cout << "E2: " << str(E2) << "\n";
cout << "D:  " << str(D) << "\n";

E1: [ 5, 10, 15, 20, 25]
E2: [ 10, 20, 30, 40, 50]
D:  [ 5, 15, 25]

Voire même d'écrire directement dans un std::set en utilisant un std::inserter et en lui demandant d'insérer à la fin, ce qui s'effectue en temps constant depuis C++11.

set<int> SD; 
std::set_symmetric_difference(E1.begin(), E1.end(), 
                              E2.begin(), E2.end(), 
                              inserter(SD,SD.end()));

cout << "E1: " << str(E1) << "\n";
cout << "E2: " << str(E2) << "\n";
cout << "SD: " << str(SD) << "\n";

E1: [ 5, 10, 15, 20, 25]
E2: [ 10, 20, 30, 40, 50]
SD: [ 5, 15, 25, 30, 40, 50]

ASD1 Notebooks on GitHub.io © Olivier Cuisenaire, 2018